When you are solving a system of the algebraic equation the echelon form and the reduced Reduced Row echelon form can be difficult to understand. There are certain conditions a matrix needs to meet to make a matrix into the echelon or to the reduced echelon form. You cna use the RREF calculator by calculator-online.net to turn a matrix into the reduced echelon and echelon form. When students are converting a matrix into the echelon form, sometimes they are not able to reduce the matrix into the echelon form.
The main reason behind that is they are not familiar with the echelon and reduced echelon form. The reduced and echelon form matrix is easy to get if you are able to convert the leading element to 1 by the multiplication of the matrices. It is easy to convert a matrix into an echleon or the reduced echelon form, but it can be a long process if you have to deal with a 3 or 4 rows matrix.
In the article below, we are defining what is echelon and the reduced echelon form of the matrix are.
What is Echelon Form?
There are certain conditions a matrix has to meet for the echelon form:
- The leading number in the matrix should be a whole number.
- The zero rows should be placed at the end of the matrix
- The second or the preceding rows from the first row should contain more zeros from the first row to the proceeding leading number.
When using the reduced echelon form calculator all the conditions are automatically applied and you have no need to covert a matrix into an echelon form or a reduced echelon form of the matrix
How to Identify the Echelon Form Matrix?
There are certain things you need to identify for the echelon and the reduced echelon form.
- First, identify the leading number in the row is a “1” an digit is also called the leading coefficient.
- The leading “1” should be the right of the one above it.
- All the rows only have zeros as the members should be at the bottom of the matrix.
An example of the Echelon form:
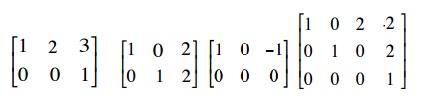
The following are not the echelon form of the matrix:
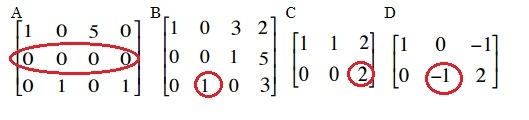
Difference between Echelon and Reduced Echelon Form?
There major difference between the echelon form matrix and the reduced echelon form matrix. The row-reduced echelon form calculator usually represents both forms of the matrix.
The major difference between the echelon and reduced echelon forms are as follows:
- In the echelon form matrix, the leading number should be in the upper right column and every non-zero should have 1. It can be possible another whole number appears in the echelon form rather than 1.
- In the reduced echelon form matrix, all the elements in the matrix should be zero or 1. In the reduced echelon form matrix, there should be only 1 or zero in a row or column.
Pivot in RREF:
The first non-zero element in each row is known to be the pivot in the row echelon form. The column in which the pivot element appears is known to be the pivot column. The RREF calculator can convert the simple matrix into a Reduced echelon form automatically.
A Matrix and its Echelon Form?
Every matrix in linear algebra has an echelon and a reduced echelon form matrix. You need to apply row reduction techniques to find the echelon and reduced echelon form of each matrix. You can use the RREF calculator to find the echelon and reduce the echelon form of a matrix easily without applying the row operation technique. There is no matrix that does have the echelon and the reduced echelon form as you need to go through a certain row operation to covert a matrix into an echelon or RREF matrix.
Conclusion:
In linear algebra, you need to convert a matrix into the row echelon form as it helps to understand the nature of the linear equation. The RREF calculator can avoid going through a lengthy procedure to convert a matrix into its echelon or reduced echelon form. You simply have to add the values of the matrix in the online tool and just press the calculate button to find the echelon form.

